what is a likelihood function?

It is no secret that statistics is a science widely used in several areas as a tool for data analysis. But this science is not only used, it is also developed in numerous areas, such as engineering, computer science, psychology, demography, social sciences and several others.

Fisher was a great example of this, this guy was a genius who lived until the middle of the 20th century, and he practically created the basis for modern statistics. But that is not my point about Fisher, what I want to draw your attention to is that he was a geneticist (you read that right, he was a geneticist) and not a statistician. Fisher is one of the greatest examples that statistics is a democratic science, which is not developed only by those with a statistical backgraund.

But the purpose of this post is not to talk about Fisher, but to explain what a likelihood function is and what it represents. I’ve been in academia since 2012, and I always realize that there are still a lot of people who don’t know what a likelihood function is, or what it represents. So the idea of this post is to clarify that. So come with me and I’ll explain!

So, the likelihood function is a function that is normally used to summarize the data. This function carries a lot of information about it, which is why we normally make the inference using it (Fisher’s idea). But let’s move on to a more formal definition of the likelihood function:

Let \(f(\mathbf{x}, \theta)\) the the joint pdf of a random sample \(\mathbf{X} = (X_1, \dots, X_n)\). So, considering that we observed \(\mathbf{X} =\mathbf{x}\) , the function of \(\theta\) defined by

\[L(\theta | \mathbf{x} ) = f(\mathbf{x}, \theta)\]

is called a likelihood function. When \(\mathbf{X}\) is independently and identically distributed, we can write

\[L(\theta | \mathbf{x} ) = \mathbf{\prod}_{i=1}^n f(x_{i}, \theta).\]

My main point here is that, although the likelihood function uses the same mathematical form as pfd, the likelihood function is a function of \(\theta\), not \(\mathbf{x}\), and this is what most confuses people. In summary, the likelihood function is not a probability function and does not measure probabilities either, the likelihood function measures how realistic it is \(\theta\) be the true parameter of the pfd of \(\mathbf{X}\).

If we compare the likelihood function at two points (say \(\theta_1\) and \(\theta_2\)) and find that

\[L(\theta_1 | \mathbf{x} ) > L(\theta_2 | \mathbf{x} )\]

so it is more likely that the sample we actually observed occurred if \(\theta = \theta_1\), than if \(\theta = \theta_2\), which can be interpreted as saying that \(\theta_1\) is a more plausible value for the true value of \(\theta\) than \(\theta_2\). We can have the same conclusion if we use the logarithm of the likelihood function (log-likelihood function). For this reason, we look for likelihood estimates, as we look for the value that is the most plausible for that dataset.

Let’s take an example. Suppose that \(X \sim N(a, b)\), with \(a = 5\) and \(b = 2\). If we look at the log-likelihood function for from \(\theta = (a, b)\) and assume that it is unknown, we get the image below

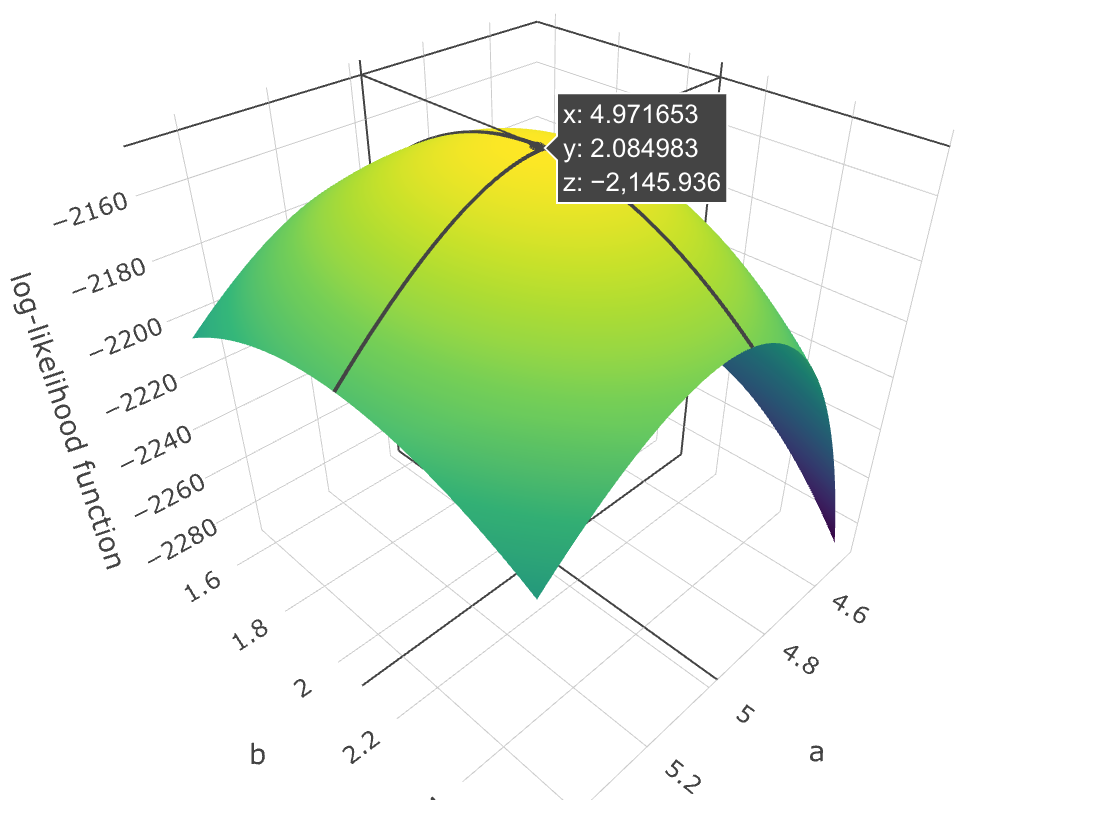
that has the maximum point \(\hat{\theta} = (4.97, 2.08)\). This maximum point is called the maximum likelihood estimate, and this value is the most plausible for \(\theta\) for this data.

Well, to sum it all up in one line, the purpose of this post was to tell you that the likelihood function is a function of the parameter and not the data, and I hope I managed to make you understand that.

I see ya in the next post, or on twitter.

References

Bolfarine, Heleno, and Mônica Carneiro Sandoval. Introdução à inferência estatística. Vol. 2. SBM, 2001.

Casella, George, and Roger L. Berger. Statistical inference. Vol. 2. Pacific Grove, CA: Duxbury, 2002.

DUDEWICZ, Edward J.; MISHRA, Satya. Modern mathematical statistics. John Wiley & Sons, Inc., 1988.